11.1 Introduction

We have already encountered the effects of atmospheric absorption in the lecture by Michel Guélin (Chapter 10). Even under low opacity conditions, observations can be difficult or impossible due to atmospheric phase fluctuations. In principle, integration of an interferometric signal is like the adding up of vectors. The amplitude is the length of a vector, and its orientation is given by the phase. Errors in the phase will cause part of the amplitudes to cancel each other out according to Eq. 11.1

$$\overline{V_{ij}^m} = V_{ij} \exp{(-\sigma^2_{\phi}/2)}$$ (11.1)

where $V_{ij}$ are the ideal visibilities, $\overline{V_{ij}^m}$ the integrated ones, and $\sigma_{\phi}$ the phase noise in radian (assuming a Gaussian noise distribution).

If our eyes were sensitive in the millimeter range with a resolving power of some arc seconds, we would not only see a luminous sky where sources are difficult to make out on the background: we would notice refracting bubbles of sizes between some centimeters to several kilometers drifting with the wind, merging, separating and distorting the view behind them. It is water vapor which has not attained the concentrations necessary for cloud formation, and mixes badly with dry air. Even in the case of low opacity and a sky clear for human perception, these distortions - which are shifts and tilts in the incoming phase front - can be so important that they make observations impossible.

In this lecture we will study the physics behind this effect and possible ways to correct for it which have become available in recent years.

The phases of a wave front that reaches ground-based observatories have been modified by their journey through refractive index variations in the Earth's atmosphere. The instrument itself has no way to tell which part of the phases are due to valuable structure in the astronomical source and which part was caused during the last kilometers in front of the telescope.

As a result, the apparent position of a point source keeps moving, so that details of an extended source become blurred (``seeing''). The perturbations become progressively decorrelated with increasing separation between two lines of sight.

Depending on turbulence scale, wavelength and telescope size, a ground-based observer will be confronted with different effects. To some extent, one can reduce unwanted perturbations by choosing an observatory's site carefully. But there are always some days which are better than others.

• If the telescope diameter is much larger than a typical turbulence cell and if phase shifts over a turbulent cell are less than 1 radian, one works in the diffractive regime: some power is scattered into an error beam, but the diffraction limited resolution of the instrument is conserved. These conditions can be found for very long baseline interferometry at cm wavelengths under good conditions.
• In the refractive regime, the turbulence cells are much larger than the telescope so that the whole image seems to move around. Phase shifts can be several radians. This is the case we have to cope with at the Plateau de Bure interferometer.
• In the intermediate case, one gets speckles on short integration times which average into an image convolved with a seeing disk (an effect well-known to optical and near infrared observers).

For a small radio telescope, the phase noise passes unnoticed (Fig.11.1).

Figure 11.1: Two single dish radio telescopes and one synthesis array observing a source. Angular resolution and the effects of atmospheric turbulence increase with the diameter of an instrument. An interferometer's synthesized beam has the same problems that a single dish with a projected baseline's diameter would experience.

Its beam size is bigger than the apparent position shifts induced by seeing, and the ray paths leading to the opposing outer edges of the reflector will not differ much. For a big single dish, the effect can become noticeable: under unstable conditions, a source may wander in and out of the beam, disturbing not only the observations of the target of interest but also pointing and focus. An interferometer suffers even more from seeing because the distances between individual antennas are large. This has the double effect of making the synthesized beam smaller and of increasing the differences in the atmospheric turbulence pattern between the optical paths. In the optical and near infrared, it is the dry atmosphere which causes the phase shifts. In the centimeter radio range, it is the tropospheric water vapor and the ionospheric plasma irregularities, and mainly water vapor in the millimeter radio range.

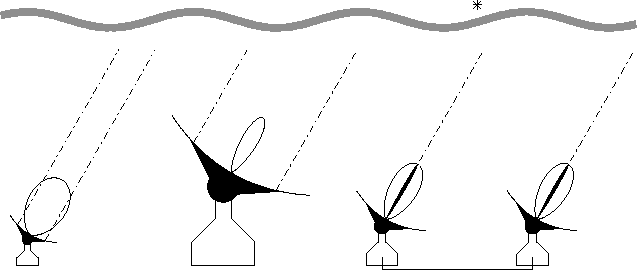The interest of interferometric phase correction is to determine and remove the atmospheric phase noise. Each individual antenna has to correct a time variable ``piston'' in the incoming wave front, which is the equivalent of adaptive optics for the synthesized dish.

Most of the water vapor is confined to the troposphere ($<$10 km) with an exponential scale height of 2 km. Its molecular weight is 18.2 g/mol so that it has the tendency to rise above dry air (28.96 g/mol). Our planet retains the water vapor due to the negative vertical temperature gradient in the troposphere, and the fact that H$_2$O is close to the transition points to liquid and solid under terrestrial pressure and temperature conditions. Venus is an example for a planet with a hot troposphere (extreme CO$_2$ and H$_2$O greenhouse effect) who lost most of its water long ago.

Under Earth's environmental conditions, water vapor mixes badly with dry air and tends to form bubbles with sizes up to several kilometers, which are broken up by turbulent motions. When choosing high and dry sites for millimeter astronomy, one must keep in mind that high phase noise can be induced even by low amounts of precipitable water.

Parameters that influence interferometric phase noise strongly are:

• wind speed,
• projected baseline length,
• the time of the day (nights are typically more stable due to the missing solar energy input to turbulence),
• topographic effects, e.g. the turbulent wakes of mountains.

Figure 11.2: Atmospheric phase noise as a function of baseline length. The position of the break and the maximum phase noise are weather dependent.

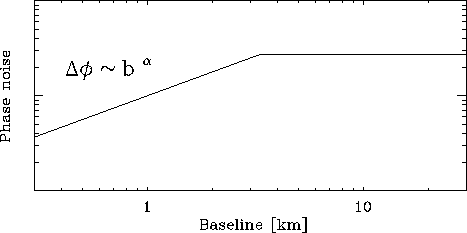The leveling off of the phase noise on a high, constant value corresponds to the outer scale size of the turbulence, where the fluctuations along two lines of sight become totally decorrelated, i.e. as bad as they can possibly get (Fig. 11.2). Increasing the baselines will not increase the phase noise any more, and this is why very long baseline interferometry can work.

In the following, some fundamentals about turbulence will be explained, and how one can analyze the properties of a turbulent atmosphere. Possible methods to monitor the phase fluctuations will be discussed, with emphasis on the phase monitoring system on the Plateau de Bure. Some examples with observational data will be presented, demonstrating its benefits and current limitations.