



Next: 3. Millimetre Very Long
Up: 2. Millimetre Interferometers
Previous: 2.5 Fourier Transform and
Contents
The 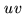 coverage
coverage
Using a Cartesian coordinate system 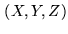 with
with 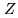 towards the pole,
towards the pole, 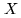 towards the meridian, and
towards the meridian, and 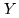 towards East, the
conversion matrix to
towards East, the
conversion matrix to 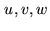 is
is
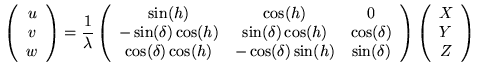 |
(2.46) |
where
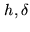 are the hour angle and declination of the phase tracking
center.
are the hour angle and declination of the phase tracking
center.
Eliminating 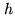 from Eq.2.46 gives the equation of an ellipse:
from Eq.2.46 gives the equation of an ellipse:
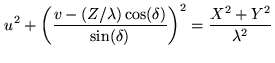 |
(2.47) |
The  coverage is an ensemble of such ellipses. The choice of antenna
configurations is made to cover the
coverage is an ensemble of such ellipses. The choice of antenna
configurations is made to cover the  plane as much as possible.
plane as much as possible.
Baseline measurement
Assume there is a small baseline error,
(
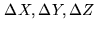 ). The phase error is
). The phase error is
Hence, if we observe 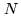 sources, we have for each source
sources, we have for each source
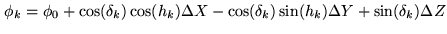 |
(2.50) |
i.e. a linear system in (
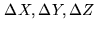 ), with
), with 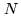 equations
and 4 unknown (including the arbitrary phase
equations
and 4 unknown (including the arbitrary phase 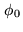 ). This can be used
to determine the baselines from phases measured on a set of sources with
known positions
). This can be used
to determine the baselines from phases measured on a set of sources with
known positions
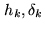 .
.
From the shape of Eq.2.49, one can see that the
determination of
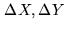 requires large variations in
requires large variations in
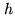 , preferably at declination
, preferably at declination
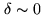 , while that of
, while that of
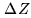 requires large variations in
requires large variations in 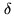 . However,
. However,
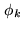 in Eq.2.50 is multi-valued (the
in Eq.2.50 is multi-valued (the 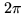 ambiguity...). Retaining the function in the [
ambiguity...). Retaining the function in the [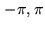 ] interval
only, the system to solve is in fact
] interval
only, the system to solve is in fact
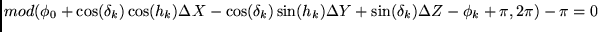 |
(2.51) |
which is a linear system of equations only if
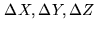 are
small enough so that the shifted modulo function is the identity. Baseline
determination usually proceeds through a ``brute force'' technique, by making a grid
search (with
are
small enough so that the shifted modulo function is the identity. Baseline
determination usually proceeds through a ``brute force'' technique, by making a grid
search (with 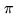 phase steps) around the most likely values for
phase steps) around the most likely values for 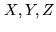 .
.




Next: 3. Millimetre Very Long
Up: 2. Millimetre Interferometers
Previous: 2.5 Fourier Transform and
Contents
Anne Dutrey
![]() coverage
coverage
![]() with
with ![]() towards the pole,
towards the pole, ![]() towards the meridian, and
towards the meridian, and ![]() towards East, the
conversion matrix to
towards East, the
conversion matrix to ![]() is
is
![]() from Eq.2.46 gives the equation of an ellipse:
from Eq.2.46 gives the equation of an ellipse:
![]() ). The phase error is
). The phase error is
![]() requires large variations in
requires large variations in
![]() , preferably at declination
, preferably at declination
![]() , while that of
, while that of
![]() requires large variations in
requires large variations in ![]() . However,
. However,
![]() in Eq.2.50 is multi-valued (the
in Eq.2.50 is multi-valued (the ![]() ambiguity...). Retaining the function in the [
ambiguity...). Retaining the function in the [![]() ] interval
only, the system to solve is in fact
] interval
only, the system to solve is in fact