In order to study the effect of the atmosphere on the outcoming longwave radiation, it is convenient to subdivide it into a ``clean dry'' component, water vapor, and aerosols (water droplets, as well as ice crystals, salt grains & dust particles, which serve as condensation seeds for water).
Table 10.1 gives the standard composition of the ``clean
dry'' air in the troposphere (i.e at altitudes ![]() km).
Except for CO
km).
Except for CO![]() , whose abundance at ground level may vary
between day and night by up to a factor of 2, this composition is
remarkably homogeneous and constant. Other trace components, most
of which are unstable (SO
, whose abundance at ground level may vary
between day and night by up to a factor of 2, this composition is
remarkably homogeneous and constant. Other trace components, most
of which are unstable (SO![]() , O
, O![]() , NO, CO, ...) have abundances
(in volume) that never exceeds 10
, NO, CO, ...) have abundances
(in volume) that never exceeds 10![]() .
.
The abundance of water is highly variable, but hardly exceeds 1% in mass, even
locally. Most of the water in the air is in the form of vapor. Even inside the
clouds, precipitation and turbulence insure that the mass of water droplets per
cm![]() seldom equals that of water vapor. In addition the water vapor mixing
ratios above 15-20 km are under 10 ppmv making it just another trace gas there.
seldom equals that of water vapor. In addition the water vapor mixing
ratios above 15-20 km are under 10 ppmv making it just another trace gas there.
Ozone and to much less extent molecular Oxygen
are responsible for most of the absorption
of the solar radiation in the UV, especially between 180 and 290 nm,
thanks to these processes:
![]() (Hartley band),
(Hartley band),
![]() (Schuman-Runge band), and
(Schuman-Runge band), and
![]() (Herzberg band),
(Herzberg band),
In the visible, the air is fairly transparent except for scattering
by aerosols, mostly water droplets, ice crystals and dust particles. In
the infrared, H![]() O, CO
O, CO![]() (around 15
(around 15 ![]() m) and O
m) and O![]() (around
10
(around
10![]() m) are very efficient absorbers of the solar and ground radiation, to
the extent that they prevent ground-based observations in large regions
of the electromagnetic spectrum.
m) are very efficient absorbers of the solar and ground radiation, to
the extent that they prevent ground-based observations in large regions
of the electromagnetic spectrum.
By clear weather, the atmospheric absorption at millimeter and submillimeter wavelengths is dominated by rotational and fine structure lines of molecules in their ground electronic and low vibrational states.
The strongest molecular rotational resonances appear in polar molecules (H![]() O
and O
O
and O![]() being the most important of such molecules in the atmosphere)
and are of the type E1 (electric dipole transitions). Intrinsically weaker M1
(magnetic dipole) transitions are of considerable practical importance in the
atmosphere due to the high abundance of O
being the most important of such molecules in the atmosphere)
and are of the type E1 (electric dipole transitions). Intrinsically weaker M1
(magnetic dipole) transitions are of considerable practical importance in the
atmosphere due to the high abundance of O![]() . We will see that collision induced
E2 (electric quadrupole) absorption involving N
. We will see that collision induced
E2 (electric quadrupole) absorption involving N![]() and O
and O![]() is measurable in the atmosphere. The different atmospheric
hydrometeors (water droplets, snow, graupel, hale, ice
cristals,...) scatter and absorb following different patterns across the
longwave (radio to submm) spectral region. All the mechanisms involved in the radiative
transfer of longwave radiation in the atmosphere will be described
in this chapter.
is measurable in the atmosphere. The different atmospheric
hydrometeors (water droplets, snow, graupel, hale, ice
cristals,...) scatter and absorb following different patterns across the
longwave (radio to submm) spectral region. All the mechanisms involved in the radiative
transfer of longwave radiation in the atmosphere will be described
in this chapter.
A mixture of ideal gases behaves like an ideal gas:
| (10.1) |
| (10.2) |
Dry air is a mixture of N![]() , O
, O![]() , ... molecules. It behaves indeed very
much like an ideal gas:
, ... molecules. It behaves indeed very
much like an ideal gas:
![]() J/mol-deg (vs 8.3149 for
an ideal gas),
J/mol-deg (vs 8.3149 for
an ideal gas), ![]() = 1.404 (vs 1.400 for ideal rigid molecules).
= 1.404 (vs 1.400 for ideal rigid molecules).
Wet air (without clouds) is a mixture of dry air + H![]() O molecules. It is customary
to denote by
O molecules. It is customary
to denote by ![]() the partial pressure of water vapor,
the partial pressure of water vapor, ![]() that of dry air, and
that of dry air, and
![]() the wet air pressure. The specific heats of water vapor are not that
different from those of ideal gases:
the wet air pressure. The specific heats of water vapor are not that
different from those of ideal gases:
![]() ;
;
![]() , vs
, vs
![]() and
and
![]() for a rigid asymmetric
top.
for a rigid asymmetric
top.
Then, Dalton's law yields:
Then, for the adiabatic expansion of a wet air bubble, one has:
At large scales, the air pressure and density depend essentially on the massive and
slowly varying dry component and are well described by hydrostatic
equilibrium. The air temperature, as we have seen, depends significantly on the
abundance and distribution of water, CO![]() (and O
(and O![]() for the stratosphere).
for the stratosphere).
At equilibrium:
For larger altitudes, from Eq.10.7 and
![]() ,
then:
,
then:
Although the above equations represent fairly well the density and pressure
throughout the troposphere, the temperature distribution can depart significantly
from the above linear variation near the ground. This ground heats up faster than the
transparent air during the day, and cools off more rapidly during the night. The
temperature gradient at low altitudes (up to 1-2 km) can be thus steeper or
shallower than described by ![]() (Kkm
(Kkm![]() ). Occasionally, it can be inverted, the
temperature increasing with altitude. The inversion layer usually stops
briskly at 1 or 2 km altitude and the normal temperature gradient resumes above.
Inversion layers are common during the night over bare land. They can also be caused
by hot winds blowing from the sea.
). Occasionally, it can be inverted, the
temperature increasing with altitude. The inversion layer usually stops
briskly at 1 or 2 km altitude and the normal temperature gradient resumes above.
Inversion layers are common during the night over bare land. They can also be caused
by hot winds blowing from the sea.
The local temperature gradient determines stability of the air to vertical motions. A rising bubble of wet air expands adiabatically as long as the water vapor it contains does not condense. Expanding, it cools almost as an ideal gas with:
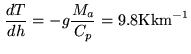
The scale height of water, ![]() , which results from a fast evaporation/condensation
process, is small (typically
, which results from a fast evaporation/condensation
process, is small (typically ![]() km) compared to the equilibrium scale height
km) compared to the equilibrium scale height
![]() km. At
km. At ![]() km, the altitude of the Plateau de Bure, the water
vapor column density
km, the altitude of the Plateau de Bure, the water
vapor column density ![]() (or
(or ![]() , ``amount of precipitable water'', when
expressed in g.cm
, ``amount of precipitable water'', when
expressed in g.cm![]() , or cm of water) is normally reduced by a factor of 3-4,
with respect to sea level. This factor, as we have seen, is strongly modulated
by the local temperature gradient.
, or cm of water) is normally reduced by a factor of 3-4,
with respect to sea level. This factor, as we have seen, is strongly modulated
by the local temperature gradient. ![]() is lower in the presence of a
low altitude inversion layer which reduces the vertical turbulence and
traps most of the water well below the observatory.
is lower in the presence of a
low altitude inversion layer which reduces the vertical turbulence and
traps most of the water well below the observatory.