The goal of this part of the calibration is to measure the atmospheric transparency above each antenna.
This calibration is done automatically and in real-time but it can be redone
a posteriori if one or several parameters are wrong using the CLIC command
ATMOSPHERE. However, for 99 % of the projects, the single-dish calibration is
correct. Moreover, we will see in this section that in most cases, even with
erroneous calibration parameters, it is almost impossible to do an error larger than
![]() .
.
For details about the properties of the atmosphere, the reader has to refer to Chapter 11 while the transmission of the atmosphere at mm wavelengths is described in Chapter 10. Most of this lecture is extracted from the documentation ``Amplitude Calibration'' by [Guilloteau 1990] for single-dish telescope and from [Guilloteau et al. 1993].
Since all this part of the calibration is purely antenna dependent
and in order to simplify the equations, the subscript ![]() will be
systematically ignored. In the same spirit, the equations will be
expressed in
will be
systematically ignored. In the same spirit, the equations will be
expressed in ![]() scale taking
scale taking
![]() (see
[Guilloteau 1990]).
(see
[Guilloteau 1990]).
The atmospheric absorption (e.g. for the lower side-band
![]() ) can be expressed by
) can be expressed by
The system temperature ![]() is given by:
is given by:
At Bure, during a standard atmospheric calibration, the measured quantities are:
Our calibration system provides then a direct measurement of ![]() and hence of
and hence of
![]() , which is deduced from quantities accurately measured. Hence, in
Eq.12.5 the only unknown parameter remains
, which is deduced from quantities accurately measured. Hence, in
Eq.12.5 the only unknown parameter remains ![]() , the opacity of the
atmosphere at zenith, which is iteratively computed together with
, the opacity of the
atmosphere at zenith, which is iteratively computed together with ![]() the
physical atmospheric temperature of the absorbing layers. This calculation is
performed by the atmospheric transmission model ATM (see Chapter 10) and
the documentation ``Amplitude Calibration'').
the
physical atmospheric temperature of the absorbing layers. This calculation is
performed by the atmospheric transmission model ATM (see Chapter 10) and
the documentation ``Amplitude Calibration'').
The opacity ![]() (or more generally
(or more generally ![]() ) comes from two terms:
) comes from two terms:
When the opacity of the atmosphere is weak (
![]() ) and equal in
both image and signal bands,
) and equal in
both image and signal bands, ![]() is mostly dependent of
is mostly dependent of ![]() and
both of them can be considered as independent of
and
both of them can be considered as independent of ![]() and hence
and hence ![]() .
.
In the conditions mentioned above, ![]() can be eliminated from Eq.12.5.
The equation becomes:
can be eliminated from Eq.12.5.
The equation becomes:
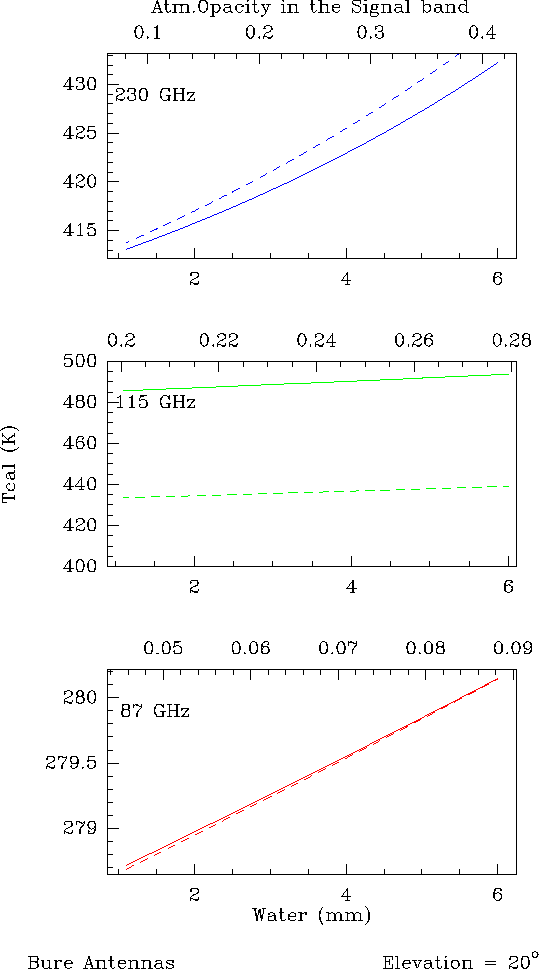
Figures 12.1 and 12.2 illustrate this point. Thick lines correspond to
the exact equation (Eq.12.5) and dashed lines to the approximation
(Eq.12.11). The comparison between Eq.12.11 and 12.5 was done for three
common cases 1) at 87 GHz, with
![]() , 2) at 115 GHz, with
, 2) at 115 GHz, with
![]() and at 230 GHz, with
and at 230 GHz, with
![]() . For the 15-m dishes, the forward efficiencies
used are
. For the 15-m dishes, the forward efficiencies
used are
![]() at 3mm and
at 3mm and
![]() at 1.3mm. Fig.12.1 is
done for a source at
at 1.3mm. Fig.12.1 is
done for a source at
![]() and Fig.12.2 for a source at
and Fig.12.2 for a source at
![]() .
.
 |
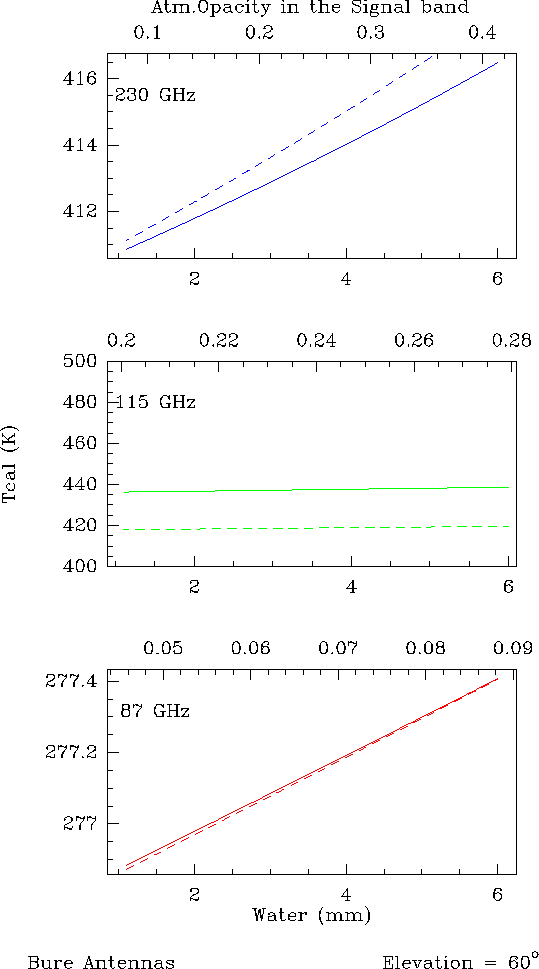 |
The following points can be deduced from these figures:
At mm wavelengths, the derivation of the ![]() (or
(or ![]() ) using an
atmospheric model is then quite safe.
) using an
atmospheric model is then quite safe.
The equations above show that ![]() is also dependent of the instrumental
parameters
is also dependent of the instrumental
parameters ![]() ,
, ![]() and
and ![]() . These parameters can also lead to
errors on
. These parameters can also lead to
errors on ![]() . Derivatives of the appropriate equations are given in the IRAM
report ``Amplitude Calibration''. Applying these equations and taking
. Derivatives of the appropriate equations are given in the IRAM
report ``Amplitude Calibration''. Applying these equations and taking
![]() K,
K,
![]() K and
K and
![]() K, the possible resulting errors
are given in the table 12.1.
K, the possible resulting errors
are given in the table 12.1.
|
As a consequence, the most critical parameter of the calibration is the Forward
Efficiency ![]() . This parameter is a function of frequency, because of optics
surface accuracy, but also of the receiver illumination. If
. This parameter is a function of frequency, because of optics
surface accuracy, but also of the receiver illumination. If ![]() is
underestimated,
is
underestimated, ![]() is underestimated and you may obtain anomalously low water
vapor content, and vice-versa.
is underestimated and you may obtain anomalously low water
vapor content, and vice-versa.
The sideband gain ratio ![]() is also a critical parameter.
is also a critical parameter. ![]() is not only
a scaling factor (see Eq.12.5), but is also involved in the derivation of the
atmospheric model since the contributions from the atmosphere in image and signal
bands are considered. This effect is important only if the opacities in both bands
are significantly different, as for the J=1-0 line of CO.
is not only
a scaling factor (see Eq.12.5), but is also involved in the derivation of the
atmospheric model since the contributions from the atmosphere in image and signal
bands are considered. This effect is important only if the opacities in both bands
are significantly different, as for the J=1-0 line of CO.
Eq.12.5 shows that as soon as the receivers are tuned in single side band
(
![]() or rejection
or rejection ![]() dB), the effect on
dB), the effect on ![]() is insignificant.
Errors can be significant when the tuning is double-side band with values of
is insignificant.
Errors can be significant when the tuning is double-side band with values of
![]() around
around
![]() . For example, when the emissivity of the sky is the
same in both bands (
. For example, when the emissivity of the sky is the
same in both bands (
![]() ), the derivative of Eq.12.8 shows
that an error of 0.1 on
), the derivative of Eq.12.8 shows
that an error of 0.1 on
![]() leads to
leads to
![]() .
.
However, this problem is only relevant to single-dish observations
and should not happen in interferometry because as soon as three
antennas are working, ![]() can be accurately measured (see
Chapter 9). At Bure the accuracy on
can be accurately measured (see
Chapter 9). At Bure the accuracy on ![]() is better
than about 1 % and the system is stable on scale of several
hours.
is better
than about 1 % and the system is stable on scale of several
hours.
Following Eq.12.5, the side band ratio will be affected by the following term:
At the same frequencies, an error of 5mm (which would be enormous) on the water vapor content will only induce an error of 1% on the gain. Around such low frequency and for small frequency offsets, the water absorption is essentially achromatic. Improper calibration of the water vapor fluctuations will then result in even smaller errors since this is a random effect.
The resulting thermal noise is given by
where ![]() is the Boltzmann's constant, A is the geometric
collecting area of the telescope,
is the Boltzmann's constant, A is the geometric
collecting area of the telescope, ![]() the global efficiency
factor (including decorrelation, quantization, etc...),
the global efficiency
factor (including decorrelation, quantization, etc...),
![]() the bandwidth in use and
the bandwidth in use and ![]() the integration time. The
resulting error on the phase determination is inversely
proportional to the signal to noise ratio, as shown in
Fig.12.3.
the integration time. The
resulting error on the phase determination is inversely
proportional to the signal to noise ratio, as shown in
Fig.12.3.