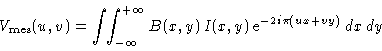15.2 Image formation in a mosaic

 

Some important mosaic properties can be understood by analyzing the combination of the data directly in the uv plane. This analysis was first proposed by [Ekers & Rots 1979]. The reader is also referred to [Cornwell 1989]. We consider a source whose brightness distribution is I(x,y) (where x and m are two angular coordinates), and whose ``true'' visibility (i.e. the Fourier transform of I) is noted V. A two-antenna interferometer, whose primary beam is B(x,y), will measure a visibility at a point (u,v) which may be written as:

$$V_{\rm mes}(u,v) = \ensuremath{\int\!\!\int} _{-\infty}^{+\infty} B(x,y)\,I(x,y)\,{\rm e}^{-2i\pi(ux+vy)}\,dx\,dy$$ (15.2)

For an observation with a phase center in (x=0,m=0) but with a pointing center in (x_p,y_p), the measured visibility (whose dependence on (x_p,y_p) is here explicitly indicated) is now:

$$V_{\rm mes}(u,v,x_p,y_p) = \ensuremath{\int\!\!\int} _{-\inft... ...infty} B(x-x_p,y-y_p)\,I(x,y)\,{\rm e}^{-2i\pi(ux+vy)}\,dx\,dy$$ (15.3)

For further use, this last relation can also be rewritten, using the symmetry properties of the primary beam B:

$$V_{\rm mes}(u,v,x_p,y_p) = B(x_p,y_p) * {\cal F}(u,v,x_p,y_p)$$ (15.4)

where * denotes a convolution product and the function $\cal F$ is defined as:

$${\cal F}(u,v,x_p,y_p) = I(x_p,y_p)\,{\rm e}^{-2i\pi(ux_p+vy_p)}$$ (15.5)

Now, imagine an ideal ``on-the-fly'' mosaic experiment: for a given, fixed (u,v) point, the pointing center is continuously modified, and the variation of the visibility with (x_p, y_p) can thus be monitored. Then, the Fourier transform of $V_{\rm mes}$ with respect to (x_p,y_p) gives (from equation 15.4):

$$\left[{\rm FT_p}(V_{\rm mes})\right](u_p,v_p) = T(u_p,v_p) \, V(u+u_p,v+v_p)$$ (15.6)

where:

• ${\rm FT_p}$ denotes the Fourier transform with respect to (x_p,y_p) and (u_p,v_p) are the conjugate variables to (x_p,y_p).

• $\left[{\rm FT_p}(V_{\rm mes})\right](u_p,v_p)$ is the Fourier transform of the observations.

• T(u_p,v_p) is the Fourier transform of the primary beam B(x_p,y_p). T is thus the transfer function of each antenna. For a dish of diameter $\cal D$, T(u_p,v_p) = 0 if $\sqrt{u_p^2+v_p^2} > {\cal D}/\lambda$.

• V(u+u_p,v+v_p) is the Fourier transform of ${\cal F}(u,v,x_p,y_p)$ with respect to (x_p,y_p). Indeed, $\cal F$ is the product of the sky brightness distribution (whose Fourier transform is V) by a phase term, and its own Fourier transform is thus simply V taken at a shifted point.

For $\sqrt{u_p^2+v_p^2} < {\cal D}/\lambda$, we can thus derive:

$$V(u+u_p,v+v_p) = \frac{\left[{\rm FT_p}(V_{\rm mes})\right](u_p,v_p)}{T(u_p,v_p)}$$ (15.7)

This relation illustrates an important property of the experiment we have considered. The observations were performed at a given (u,v) point but with a varying pointing center. Equation 15.7 shows that is possible to derive from this data set the visibility V(u+u_p,v+v_p) at all (u_p,v_p) which verify $(u_p^2+v_p^2)^{1/2} < {\cal D}/\lambda$. In other terms, the measurements have been done at (u,v) but the redundancy of the observations allows to compute (through a Fourier transform and a division by the antenna transfer function) the source visibility at all the points of a disk of radius ${\cal D}/\lambda$, centered in (u,v).

Interpretation

In very pictorial terms, one can say that the adjacent pointing reinforce each other and thereby yield a estimate of the source visibility at unmeasured points. Note however that the resulting image quality is not going to be drastically increased: more information can be extracted from the data, but a much more extended region has now to be mapped^15.2. The redundancy of the observations has only allowed to rearrange the information in the uv-plane. This is nevertheless extremely important, as e.g. it allows the estimate part of the missing short-spacings (see below).

How is it possible to recover unmeasured spacings in the uv-plane? It is actually obvious that two antennas of diameter $\cal D$, separated by a distance $\cal B$, are sensitive to all the baselines ranging from ${\cal B}-{\cal D}$ to ${\cal B}+{\cal D}$. The measured visibility is therefore an average of all these baselines: $V_{\rm mes}$ is actually the convolution of the ``true'' visibility by the transfer function of the antennas. This is shown by the Fourier transform of equation 15.2, which yields: $V_{\rm mes} = T*V$. Now, if the pointing center and the phase center differ, a phase gradient is introduced across the antenna apertures, which means that the transfer function is affected by a phase term. Indeed, the Fourier transform of equation 15.3 yields:

$$V_{\rm mes}(u,v) = \left[T(u,v)\,{\rm e}^{-2i\pi(ux_p+vy_p)}\right]* V(u,v)$$ (15.8)

Hence, the measured visibilities are (still) a linear combination of the ``true'' visibilities. Measurements performed in various directions (x_p,y_p) give many such linear combinations. One can thus expect to derive from this linear system the initial visibilities, in the baseline range from ${\cal B}-{\cal D}$ to ${\cal B}+{\cal D}$. Equation 15.7 just shows that a Fourier transform allows to do that.

Field spacing in a mosaic

In the above analysis, a continuous drift of the pointing center was considered. However, the same results can be reached in the case of a limited number of pointings, provided that classical sampling theorems are fulfilled. We want to compute the visibility in a finite domain, which extends up to $\pm {\cal D}/\lambda$ around the nominal center, and therefore the pointing centers have to be separated by $\lambda/2{\cal D}$ (see [Cornwell 1988]). In practice, the (gaussian) transfer function of the millimeter dishes drops so fast that one can use without consequences a slightly broader, more convenient sampling, equal to half the primary beam width (i.e. $1.2\,\lambda/2{\cal D}$).

Mosaics and short-spacings

As with any other measured point in the uv plane, it is possible to derive visibilities in a small region (a disk of diameter ${\cal D}/\lambda$) around the shortest measured baseline. This is the meaning of the statement that mosaics can recover part of the short-spacings information: a mosaic will include (u,v) points corresponding to the shortest baseline minus ${\cal D}/\lambda$.

In practice, however, things are more complex. First, we have to deal with noisy data. As a consequence, it is not possible to expect a gain of ${\cal D}/\lambda$: the transfer function T which is used in equation 15.7 is strongly decreasing, and therefore signal-to-noise ratio limits the gain in the uvplane to a smaller value, typically ${\cal D}/2\lambda$ ([Cornwell 1988]). This is still a very useful gain: for the Plateau de Bure interferometer, this corresponds to a distance in the uvplane of 7.5 m, while the shortest (unprojected) baseline is 24 m. Secondly, the analysis described above would be rather difficult to implement with real observations. Instead, one prefers to combine the observed fields to directly reconstruct the sky brightness distribution. The resulting image should include the information arising from the redundancy of the adjacent fields, among them part of the short-spacings. However, the complexity of the reconstruction and deconvolution algorithms that have to be used precludes any detailed mathematical analysis of the structures of the maps. For instance, the (unavoidable) deconvolution of the image can also be interpreted as an interpolation process in the uv plane (see [Schwarz 1978]) for the case of the CLEAN algorithm) and its effects can thus hardly be distinguish from the intrinsic determination of unmeasured visibilities that occur when mosaicing.