



Next: 2.5 Fourier Transform and
Up: 2. Millimetre Interferometers
Previous: 2.3 Delay Tracking and
Contents
With the Earth rotation, the cosine term of Eq.2.22 modulates
the correlator output quasi-sinusoidaly with a natural fringe rate of
which is of order of 10 Hz for b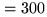 m baselines and
m baselines and
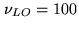 GHz. Note that the fringe rate only depends on the
effective angular resolution (
GHz. Note that the fringe rate only depends on the
effective angular resolution (
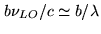 is
the angular resolution,
is
the angular resolution, 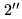 in the above example).
in the above example).
The fringe rate is somewhat too high for simple digital sampling
of the visibility. An exception is VLBI (because there is no other
choice), although the resolutions are 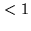 mas. The usual
technique is to modulate the phase of the local oscillator
mas. The usual
technique is to modulate the phase of the local oscillator
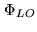 such that
such that
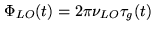 at
any given time. Then Eq.2.25 is reduced to
at
any given time. Then Eq.2.25 is reduced to
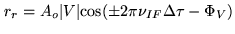 |
(2.28) |
(with the + sign for USB conversion, and the - sign for LSB
conversion), is a slowly varying output, which would be constant
for a point source at the reference position (or delay tracking
center). This process is called Fringe Stopping, since it
stops the fringe pattern modulation.
After fringe stopping, we can no longer measure the amplitude 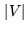 and the phase
and the phase
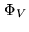 separately, since
separately, since 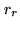 is now a constant for a point source. A modulation
of the delay tracking could be used to separate
is now a constant for a point source. A modulation
of the delay tracking could be used to separate 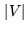 and
and 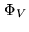 . Instead, it is
more convenient and effective to use a second correlator, with one signal phase
shifted by
. Instead, it is
more convenient and effective to use a second correlator, with one signal phase
shifted by 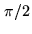 . Its output is
. Its output is
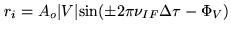 |
(2.29) |
With both correlators, we measure directly the real 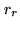 and
imaginary
and
imaginary 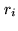 parts of the complex visibility
parts of the complex visibility 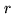 . The device is
thus called a ``complex'' correlator.
. The device is
thus called a ``complex'' correlator.
Note:
From Eq.2.28, a delay tracking error
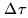 appears as
a phase slope as a function of frequency, with
appears as
a phase slope as a function of frequency, with
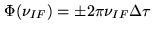 |
(2.30) |




Next: 2.5 Fourier Transform and
Up: 2. Millimetre Interferometers
Previous: 2.3 Delay Tracking and
Contents
Anne Dutrey
![]() mas. The usual
technique is to modulate the phase of the local oscillator
mas. The usual
technique is to modulate the phase of the local oscillator
![]() such that
such that
![]() at
any given time. Then Eq.2.25 is reduced to
at
any given time. Then Eq.2.25 is reduced to
![]() appears as
a phase slope as a function of frequency, with
appears as
a phase slope as a function of frequency, with