12.3 Flux Calibration (visitor's nightmare)

More details are found in the documentation ``Flux measurement with the IRAM Plateau de Bure Interferometer'' by A.Dutrey & S.Guilloteau.

12.3.1 Introduction

Because of the focus and pointing errors, and possible drifts in receiver gains, amplitude calibration has always been difficult at mm wavelengths. In addition to these basic single-dish effects, the variable amount of decorrelation introduced by phase noise (atmospheric and/or instrumental) make it difficult, if not impossible, for an interferometer to measure absolute flux densities.

All measurements need to be relative to some source of known flux. In practice, planets are used because they are among the few astronomical objects sufficiently strong at millimeter wavelengths for which flux density predictions are possible and sufficiently accurate. They are then used as primary calibrators to bootstrap the flux of the stronger quasars which are point sources. Since the quasars are highly variable, a regular monitoring (each month) is needed. These observations require a very good weather with a small amount of precipitable water vapor ($<$ 4 mm) and a stable atmospheric phase. If not properly taken into account, the quasar variability can produce an error in the flux scale during one configuration which does not result in a simple scale factor in the final image, but introduces artifacts.

12.3.2 Calibration procedure at Bure

12.3.2.0.1 Some basic points

Because of the physics of quasars, the spectral index may be variable with time as the source intensity. Simultaneous measurements at 2 frequencies are thus needed to estimate it accurately, IRAM instruments (30-m and PdBI) use the frequencies of 86.7 GHz and 228 GHz. At the 30-m, flux density measurements are done during the pointing sessions while they are performed in special sessions at Bure, usually after baseline measurements.

The results of the flux sessions are regularly reduced and published in an internal report (usually each 4 months). These reports are currently available on the web, in the local IRAM page (see).

12.3.2.0.2 How we proceed at Bure

In practice, it is impossible (and not necessary) to follow all the quasars used as amplitude calibrator at the IRAM interferometer. Monitoring of the RF bandpass calibrators which are strong quasars with flux density $>2$ Jy (no more than 4-8 sources) is enough. In the meantime, planets are observed as primary calibrators. These sessions require to calibrate the atmosphere ($T_{sys}$) on each source and to check regularly the focus.

At the Bure interferometer, the flux density measurements on quasars are done by pointings in interferometric mode. Pointings on planets are actually done in total power mode because they are resolved by interferometry and strong enough. Total power intensity is not affected by the possible decorrelation due to atmospheric phase noise. However, it is then necessary to accurately determine the efficiencies of the individual antennas (conversion factor in Jy/K) in interferometric mode ( $\ensuremath{\mathcal{J}}_I$) and in single-dish mode ( $\ensuremath{\mathcal{J}}_S$).

12.3.2.0.3 Determining the antenna efficiencies (Jy/K)

For each flux session, $\ensuremath{\mathcal{J}}_S$ is measured on planets by comparison with the models (see GILDAS programs ASTRO or FLUX).

For a given antenna, the interferometric efficiency $\ensuremath{\mathcal{J}}_I$ is always $\geq \ensuremath{\mathcal{J}}_S$. Pointing measurements in interferometric mode are not limited by the atmospheric decorrelation because the timescale of the atmospheric decorrelation is usually significantly larger than the time duration of the basic pointing integration time ($<$ a few sec). On the contrary, all instrumental phase noise on very short timescale can introduce a significant decorrelation and degrades $\ensuremath{\mathcal{J}}_I$. This is what may happen from time to time at a peculiar frequency due to a bad optimization of the receiver tuning.

For example, in the initial 1.3mm observations, strong decorrelation was introduced by the harmonic mixer of the local oscillator system which degraded $\ensuremath{\mathcal{J}}_I$ by a factor of $2-4$ depending of the antennas. This problem has been solved recently. Now at 3mm, it is reasonable to neglect the instrumental noises and take $\ensuremath{\mathcal{J}}_I = \ensuremath{\mathcal{J}}_S$. At 1.3mm, the new harmonic mixers have been installed only recently and statistics on the site are rare but laboratory measurements show that the loss in efficiency should be small. The Table 12.2 gives the antenna efficiencies $\ensuremath{\mathcal{J}}_S$, as measured in flux sessions or by holography.

Table 12.2: Conversion factor from K to Jy for the 15-m antennas of Plateau de Bure

Antenna	3mm efficiency	1.3mm efficiency
number	(Jy/K)	(Jy/K)
1	22	37
2	21	27
3	21	36
4	21	29
5	22	34

These values are the current efficiencies (as of November 1997); older values are given in flux reports. They assume that the focus is optimum and do not include any instrumental phase noise. $\ensuremath{\mathcal{J}}_I$ agrees usually within 10 % at 3mm and 15 % at 1.3mm with $\ensuremath{\mathcal{J}}_S$, note that $\ensuremath{\mathcal{J}}_I$ must be $\geq \ensuremath{\mathcal{J}}_S$.

Being able to cancel out most of the instrumental phase noise even at 1.3mm makes the IRAM interferometer a very reliable instrument. It is reasonable to think that, in the near future, the flux calibration will be systematically performed at Bure at the beginning of each project by reference to the antenna efficiencies. This is indeed already the case: after pointing and focusing, we systematically measure the flux of calibrators when starting a new project (data labeled FLUX in files). Up to now, for typical weather conditions, most (more than 90 %) of the flux measured at 3mm are correct within 10 % and more than 60 % at 1.3mm are within 15 %.

12.3.2.0.4 CRL618 and MWC349 as secondary flux calibrators

Finally, for each project, a complementary flux check is systematically done using the continuum sources CRL618 or MWC349 (pointing + cross-correlations). However these sources must be used with some caution. CRL618 is partially resolved in A and B configurations at 3mm and in A,B,C at 1.3mm. Moreover it has strong spectral lines which may dominate the average continuum flux; this must be checked before using it for flux estimates. MWC349 is unresolved and remains a reliable reference in all antenna configurations. The only strong lines for MWC349 are the Hydrogen recombination lines. The adopted flux densities are:

For CRL618 (see flux reports 13 and 15):

• CRL618 F(87 GHz) = 1.55 Jy ($+/-0.15$)
  At 87 GHz, the flux density of CRL618 (free-free emission from the HII region) has increased since 1990 (where it was $\sim$ 1.1 Jy instead of 1.55 Jy).
• CRL618 F(231.9 GHz) = 2.0 Jy ($+/-0.3$),
  from [Martin-Pintado et al. 1988]. Since the flux density has increased at 87 GHz, this value needs to be observationally confirmed. Beware of the line contamination which can be high in CRL618.

For MWC349:

• Spectrum of MWC349 F $(\nu ) = 1.69(\nu/227 {\rm GHz})^{0.6}$
• MWC349 F(87 GHz) = 0.95 Jy
• MWC349 F(227 GHz) = 1.69 Jy

These values agree within 1 $\sigma$ with the measurement performed at 87 GHz [Altenoff et al. 1994], (0.87 $\pm 0.09$ Jy).

12.3.3 Determining the absolute flux scale on a project

12.3.3.0.1 The method

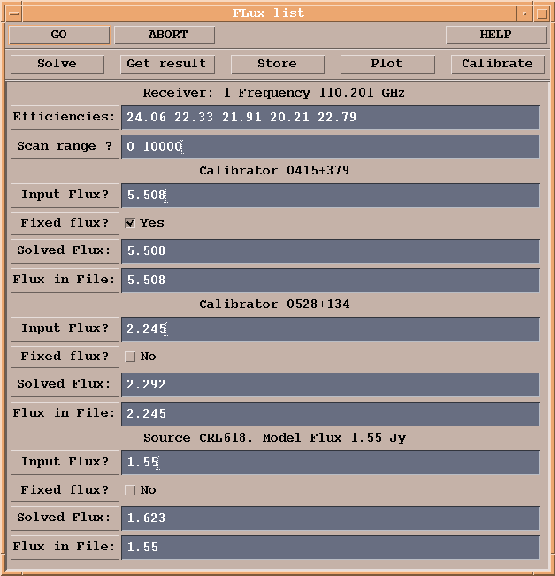
Fig.12.4 is a printout of the ``standard calibration procedure'' used in CLIC. This procedure uses the CLIC command SOLVE FLUX which works on cross-correlation only as follows:

1. The flux of the reference source is fixed to $F(\mathrm{Ref})$
2. $F(\mathrm{Ref})$ is used to measure the antenna efficiency by dividing it by antenna temperature of the reference ( $T_A^*(\mathrm{Ref})$): $\ensuremath{\mathcal{J}}_I= F(\mathrm{Ref}) / T_A^*(\mathrm{Ref})$
3. $\ensuremath{\mathcal{J}}_I$ is used to compute the flux of all other sources in the index: $F(source) = \ensuremath{\mathcal{J}}_I \times T_A^*(source)$

The flux density of the amplitude calibrators will be used in the final step of the amplitude calibration to fix the flux of the source of astronomical interest.

12.3.3.0.2 The practice

In the automatic procedure, the reference sources are the calibrators where Fixed flux is set to YES and the reference values are in the variable Input Flux. Flux in file corresponds to the value stored with the data (by using the observational command FLUX, see Chapter 8 for details). The calculation is performed by clicking on SOLVE and the results are displayed inside the variable Solved Flux.

If you want to iterate using one of these values as reference, you need to write it in the variable Input Flux and set Fixed flux to YES. Like in the CLIC command SOLVE FLUX, the individual antenna efficiencies ( $\ensuremath{\mathcal{J}}_I$) are computed; these values are only averaged values on the time interval using all sources. They are then affected by many small biases like pointing or focus errors and atmospheric decorrelation and they are usually worse than the canonical values given in table 12.2 (for biases, see end of this section).

When you are satisfied by the flux calibration, you need to click on the following sequence of buttons: 1) Get Results in order to update the internal variables of the CLIC procedure, 2) Store to save the flux values inside the header file (hpb file) and 3) Plot to display the result of your calibration. The plot shows the inverse of the antenna efficiencies ( $1/\ensuremath{\mathcal{J}}_I$) versus time for all selected sources. If the flux calibration is correct, all sources must have the same value e.g. $1/\ensuremath{\mathcal{J}}_I$. This plot is systematically done in mode amplitude scaled (written on the top left corner). In this mode, the antenna temperature of each source $T_A^*(source)$ in K is divided by its assumed (variable Input flux) flux density $F(source)$ in Jy (the value you have just stored), the result is then $T_A^*(source)/F(source)= 1/\ensuremath{\mathcal{J}}_I(source)$ which must be the same for all sources and equal to $1/\ensuremath{\mathcal{J}}_I$. If it is not the case, for example if one source appears systematically lower or higher than the others, this means that its flux is wrong and you need to iterate.

Note that the scan range, applied on all calibrators, which is by default the scan range of the ``standard calibration procedure'' can be changed. This option is useful when there is some shadowing on one calibrator because the shadowing can strongly affect the result of a SOLVE FLUX. If you change the scan range, do not forget to click on UPDATE.

Figure 12.4: User interface of the ``standard calibration procedure'' of CLIC corresponding to the flux calibration.

12.3.4 Possible biases and remedies

12.3.4.0.1 Flux densities are more important than efficiencies

In the final amplitude calibration performed on the source (see next section), the flux of the source is determined by reference to the flux of the amplitude calibrator which is usually also the phase calibrator. This means that the averaged efficiencies $\ensuremath{\mathcal{J}}_I$ computed by SOLVE FLUX and the automatic procedure are not directly used and in many case variations of $\ensuremath{\mathcal{J}}_I$ does not affect the accuracy of the final amplitude calibration because they are corrected. It is then fundamental to have a good estimate of the flux of the amplitude calibrator but not necessarily to know precisely the averaged $\ensuremath{\mathcal{J}}_I$.

12.3.4.0.2 Possible biases

Using the automatic procedure, the following biases may occur:

1. There is some shadowing on the reference source. The estimate of the $\ensuremath{\mathcal{J}}_I$ can then be wrong: use another reference.

2. One or several antennas are off focus: $\ensuremath{\mathcal{J}}_I$ is larger than $\ensuremath{\mathcal{J}}_S$ but flux densities can still be correct if there is no significant focus drift during the time interval used to measure the fluxes. If the data are affected by a significant focus drift, this also affects the accuracy of the flux measurements. Depending of the observation time of the reference and of the sources, the estimated flux densities can be either too low (reference taken at the beginning when the focus is correct, sources at the end when the focus is off) or too high (opposite situation). In both cases, it is necessary to check the focus (or have a look at the show.ps file). If no drift occurs, the measured fluxes are correct. If a drift occurs, the flux calibration must be done on a smaller interval of time where the focus drift remains negligible.

3. The pointing on the reference is bad. $\ensuremath{\mathcal{J}}_I$ is then overestimated implying that the flux of all other sources (with good pointing) is also overestimated. Check the pointing on the possible reference sources (or see the show.ps file) and select a better reference.

4. There is a strong atmospheric decorrelation because flux measurements are performed on cross-correlations of about 4 minutes when the atmospheric phase fluctuations are high (check them on an individual cross-correlation taken on a strong quasar e.g. the RF calibrator). There are two possibilities: i) when the atmospheric correction works well (as it is usually the case), just apply it to measure the fluxes; ii) if not, the data may be usable at 3mm by selecting the best scans on a small interval of time but at 1.3mm data are useless.

5. The interferometric efficiencies $\ensuremath{\mathcal{J}}_I$ are really very different to $\ensuremath{\mathcal{J}}_S$ because there is a wonderful mixing of the points mentioned above... Ask to an expert (e.g. your local contact...).

Note that the biases 3) and 4) do not affect flux estimates when they are performed on pointing data (as in sessions of flux measurements).

12.3.5 The program FLUX

This program is not used by the external users of the PdBI but IRAM astronomers to provide reliable flux density of quasars to visitors (see flux reports). A description of the program is given in ``Flux measurement with the IRAM Plateau de Bure Interferometer'' by A.Dutrey & S.Guilloteau