10.4 Atmospheric absorption evaluation

Calculations of zenith atmosphere opacity at 2.5 and 2.9 km, the altitude of the IRAM sites, can be performed with the updated ATM model [Pardo et al. 2001b] (see Figure 10.4). In fact, the model itself has been installed on-line on the IRAM telescopes of Pico Veleta and Plateau de Bure; it is activated at each calibration or skydip and allows to interpret the observed sky emissivity in terms of water and oxygen contributions and of upper and lower sideband opacities. Note that the opacities derived from sky emissivity observations do not always agree with those calculated from the measurement of $P, T,$ and the relative humidity on the site, as water vapor is not at hydrostatic equilibrium.

The typical zenith atmospheric opacities, in the dips of the 1.3 mm and 0.8 mm windows (e.g. at the frequencies of the $J=2-1$ and $3-2$ rotational transitions of CO, 230.54 and 345.80 GHz ), are respectively 0.15-0.2 and 0.5-0.7 in winter at the IRAM sites. The astronomical signals at these frequencies are attenuated by factors of respectively $\simeq 1.2$ and 2 at zenith, 1.3 and 2.8 at 45 degree elevation, and 1.7 and 6 at 20 degree elevation. Larger attenuations are the rule in summer and in winter by less favorable conditions. The $J=1-0$ line of CO, at 115.27 GHz, is close to the 118.75 GHz oxygen line. Although this latter is relatively narrow, it raises by $\simeq$0.3 the atmosphere opacity (which is 0.35-0.4). The atmosphere attenuation is then intermediate between those at 230 and 345 GHz (by dry weather, however, it is more stable than the latter, since the water contribution is small). The measurement of accurate CO line intensity ratios (even not considering the problems linked to differences in beam size and receiver sideband gain ratios) requires therefore good weather, a high source elevation, and a careful monitoring of the atmosphere.

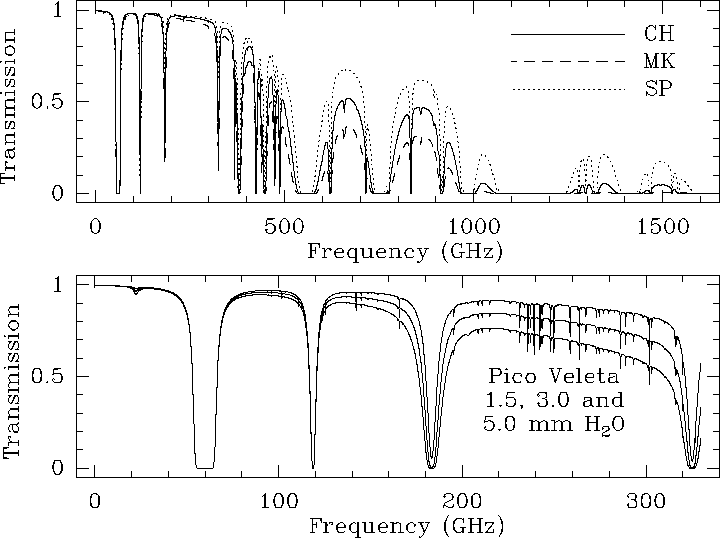
During the past few years, new ground-based astronomical observatories have been built to allow access to the submillimeter range of the electromagnetic spectrum. Potential sites are now being tested for more ambitious instruments such as the Atacama Large Millimeter Array (ALMA). All of these are remote, high altitude sites. For our simulations we have selected three sites of interest for submillimeter astronomy: Mauna Kea, HI, USA (LAT=19:46:36, LONG=-155:28:18; home of the Caltech Submillimeter Observatory, James Clerk Maxwell Telescope and Submillimeter Array), Chajnantor, Chile (LAT=-23:06, LONG=-67:27; site selected for ALMA) and the Geographic South Pole (site of the Antarctic Submillimeter Telescope and Remote Observatory). The results of this comparison are also shown on Figure 10.4.

Figure 10.4: Calculated zenith atmospheric transmissions and continuum-like opacities for Mauna Kea, Chajnantor and the South Pole corresponding to the 1$^{st}$ quartile of the cumulative water column statistics for winter time in the three sites. The H$_{2}$O cumulative distributions used here were derived from different methods leading probably to a comparative optimistic result for the South Pole. For comparison we have added the expected transmission in the millimeter range for Pico Veleta in winter for 1.5, 3.0 and 5.0 mm of water vapor.

10.4.1 Correction for atmospheric absorption, $T_A^*$

By analogy with the Rayleigh-Jeans approximation, $I= 2kT/\lambda^2$, which strictly applies to long wavelengths, the mm-wave radio astronomers have introduced the concept of ``radiation'' or ``effective'' temperatures, which scale linearly with the detected power.

The noise power detected by the telescope is the sum of the power received by the antenna, ${\mathcal{W}}_{A}$, and of the noise generated by the receiver and transmission lines, ${\mathcal{W}}_{rec}$.

Using Nyquist's relation ${\mathcal{W}} = kT \Delta\nu$, ${\mathcal{W}}_{A}$ and ${\mathcal{W}}_{rec}$ can be expressed in terms of the temperatures $T_A$ and $T_{rec}$ of two resistors, located at the end of the transmission line, which would yield noise powers equal to ${\mathcal{W}}_{A}$ and ${\mathcal{W}}_{rec}$, respectively: ${\mathcal{W}}_A + {\mathcal{W}}_{rec} = k T_A \Delta\nu + k T_{rec} \Delta\nu = k (T_A + T_{rec}) \Delta\nu$.

$T_A$ is called the ``antenna temperature'' and $T_{rec}$ the ``receiver temperature''. $T_A$ becomes $T_{load}$ when the receiver horn sees a load, instead of the antenna, and $T_{gr}$ when it sees the ground. It should be noted that $T_{load}$ and $T_{gr}$ are not stricto sensus equal to the load and ground physical temperatures, but are only ``Rayleigh-Jeans'' equivalent of these temperatures (they are proportional to the radiated power). For ambient loads, they approach closely the physical temperature, since $h\nu /k\simeq 11$ K at $\lambda= 1.3$ mm.

When observing with the antenna a source and an adjacent emission-free reference field, one sees a change $\Delta T_A= T_A(sou) - T_A(ref)$ in antenna temperature. Because of the calibration method explained below, it is customary, in mm-wave astronomy, to replace $\Delta T_A$, the source antenna temperature, by $\Delta T_A^*$, the source antenna temperature corrected for atmosphere absorption and spillover losses. Both are related through: $T_A = (1-\eta_f) T_{gr} + \eta_f (T_{sky}+ \Delta T_A^* e^{-\tau})$, where $\tau$ is the line-of-sight atmosphere opacity. $\eta_f$ is the forward efficiency factor, which denotes the fraction of the power radiated by the antenna on the sky (typically of the order of 0.9, see also Chapter 1).

The source equivalent ``radiation temperature'' $T_R$ (often improperly called ``brightness temperature'' and therefore denoted $T_{MB}$ when it is averaged over the main beam) and $\Delta T_A^*$ are related through

$$\Delta T_A^* =\int _{sour}T_R {\mathcal{A}}(x,y)dxdy$$

where ${\mathcal{A}}(x,y)$ is the antenna power pattern. For a source smaller than the main beam, $\Delta T^*_A = \eta_b/\eta_f T_{MB}$ (where $\eta_b$ is the beam efficiency factor, see also Chapter 1).

When observing a small astronomical source with temperature $\Delta T_{R}» T_{BG}=2.7$ K, located at an elevation $el$, one detects a signal ${\cal V}_{sour}$ (of scale: ${\cal G}$ volt or counts per Kelvin):

$$\frac{{\cal V}_{sour}}{\cal G}=M_{sour}= T_{rec}+ (1-\eta_{f})T_{gr}+\eta_{f} T_{sky}+ \eta_{b} T_{MB}\times e^{-\tau}$$ (10.27)

This signal can be compared with the signals observed on the blank sky ($T_{atm}$), close to the source, and to that observed on a hot load ($T_{load}$):

$$M_{atm} = T_{rec} +(1-\eta_{f})T_{gr}+\eta_{f} T_{sky}; \;\;\; T_{sky} = (1-e^{-\tau})T_{atm}; \;\;\; M_{load} = T_{rec} + T_{load}$$ (10.28)

here, we have neglected the cosmic background and assume, in a first step, that the receiver is tuned single sideband.

10.4.1.1 Simplest case

(e.g. [Penzias & Burrus 1973])

Let's assume that $T_{load}\simeq T_{gr}\simeq T_{atm}$; then:

$$M_{load}-M_{atm} = \eta_f T_{gr} e^{-\tau}$$

$$M_{sour}-M_{atm} = \Delta T_{A}^* e^{-\tau}$$

$$\Delta T_{A}^* = \frac{M_{sour}-M_{atm}}{M_{load}-M_{atm}} \eta_{f} T_{gr}$$ (10.29)

Note that in Eq.10.29, the measurement of the antenna temperature includes the atmospheric opacity correction, but does not depend explicitly on an assumption on the atmospheric opacity. We can write:

$$\Delta T_A^*= \frac{M_{sour}-M_{atm}}{M_{load}-M_{atm}}{\bf T_{cal}}$$ (10.30)

where we define $T_{cal}$ as $T_{cal}= \eta_f T_{gr} \simeq \eta_f T_{atm}$.

10.4.1.2 More realistic case

Typically, the mean atmosphere temperature is lower than the ambient temperature near the ground by about 40 K: $T_{atm} \simeq T_{gr} - 40 {\mathrm K}$; then, the formula above still holds if we replace $T_{cal}$ by:

$$T_{cal} = ({T_{load}- T_{emi}})e^\tau$$ (10.31)

$$\mathrm{with } T_{emi} = T_{sky} \eta_f+ (1-\eta_f) T_{gr}$$

$$= \frac{(T_{load}+ T_{rec})\times M_{atm}}{M_{load}}-T_{rec}$$ (10.32)

$$\T_{sky} = (1-e^{-\tau})(T_{gr}-40)$$

$T_{rec}$, the receiver effective temperature is usually calculated by the $Y$ factor method using a cold load (usually cooled in liquid nitrogen, i.e. at 77 K) and an ambient load (e.g. at 290 K).

$$Y = \frac{M_{hot\_load}}{M_{cold\_load}} \;\;\;\;\;\;\; T_{rec} = \frac{T_{hot\_load}-Y T_{cold\_load}}{Y-1}$$ (10.33)

10.4.1.3 General case

The receiver is not purely single-sideband. Let us denote by $G^l$ and $G^u$ the normalized gains in the receiver lower and upper sidebands, $G^l + G^u = 1$. The atmosphere opacity per km varies with altitude as does the air temperature.

Then, the above expressions of $T_{sky}$ and $T_{emi}$ should be explicited for each sideband ($j= u$ or $l$):

$$T_{sky}^j = (1-e^{-{\tau}^j}) T_{atm}^j$$ (10.34)

$$T_{emi} = T_{sky}^l \eta_f G^l + T_{sky}^u \eta_f G^u+ (1-\eta_f) T_{gr}$$ (10.35)

The atmospheric transmission model ATM allows to calculate iteratively $\tau_\nu$ from a load+ sky measurement. The values of $\tau^l, \tau^u$ are calculated for the Standard US atmosphere (parameters are: Winter-, Spring-, or Summer-temperature $T$, altitude, latitude, water vapor $w$) by summing up the contributions of O$_2$, H$_2$O and O$_3$ (including rare isotopes and vibrationally excited states). A first guess of the amount of precipitable water is made from the ambient temperature, pressure and humidity. Then, the expected $T_{sky}$ and $T_{emi}$ are calculated from the two expressions above and $T_{emi}$ is compared to its value measured from the the observation of the atmosphere and the load (Eq.10.32). The value of $w$ is changed and the calculation of $\tau^j, T_{sky}^j$ and $T_{emi}$ restarted. Normally, the process converges after 2 to 4 iterations. Once $w$ and $T_{emi}$ are known, the calibration factor $T_{cal}$ can be derived

$$T_{cal}^j = ({T_{load} - T_{emi}})e^{\tau^j}$$ (10.36)

and the data calibrated in the $T_A^*$ scale using Eq.10.30.